Turtle Graphics takes its name from the animal, and the idea is that you imagine a turtle with a pencil on its back, and how it would move through space given a series of instructions. As such, turtle graphics are used to graphically interpret L- Systems. 3D - turtle interpretations are different from those in 2D in that positions are represented by Geometric Vectors. If you think about these vectors as three unit vectors, H,L,U, and say that these are perpendicular to each other, you have a fairly common way of portraying the movements of a 3D turtle. The H stands for 'heading', the L for 'left', and the U stands for 'up'.(Illustration).

The turtle is way of imagining movement in space. Turtle movements are produced from strings of words from a grammar, and the idea is to portray images of physical phenomena. The string- interpretation into turtle movement is usually one according to the one mentioned above.

The rotation matrices for the rotation of the 3D turtle come in a form like this:

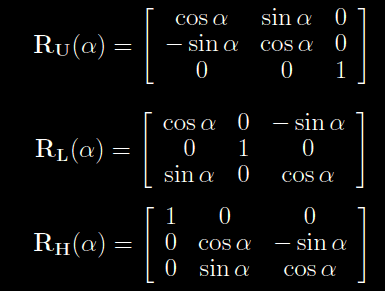
Here the angle is parameter and the RU is the TURN LEFT or TURN RIGHT of the turtle(LEFT=+, RIGHT = -). Also, there are symbols used for pitch, roll and turn-around: The RL is the PITCH of the turtle( & = pitch down , ^ = pitch up). The RH is the ROLL of the turtle(\ = roll left, /= roll right) and The TURN – around turtle( | =Turn-around(RU(180)))

For RU, the theoretical "x" axis remains as zero value, while left and right are calculated as values of cos(angle) and sin(angle) .

For RL, the pitch is calculated nearly the same, if you consider the UP and DOWN simply as another version of LEFT and RIGHT.

For RH, the calculation can be thought of as pitching the turtle 90 degrees, and then applying the RU matrix, just done all in the RH – matrix.

Going further into the math of matrices: The above mentioned matrices calculate states of a turtle, and this turtle in turn makes moves of a certain set distance . But how are the matrices calculated ?Well, first of all in computer Graphics we are dealing with the viewpoint in addition to the three dimensions, so we So what are we doing when we are playing with 3D software? Without giving it much thought we are actually constantly producing calculations of lengths and angles using trigonometry.

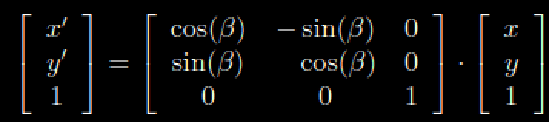
Consider rotating a 2D point (x,y) around the origin of a coordinate system by 90 degrees: You would be given a matrix such as the one above. The new point (x',y') would be calculated by a matrix following the logic below, using either triangle or circle trigonometry.

What you are seeing here can be explained like this :

- Take the ratio between the opposite side and the hypotenuse in a hypothetical "right triangle" according to your coordinate system and multiply it by the original x coordinate.(Call this Sum A) Then take the negative value of the ratio between opposite side and hypotenuse and multiply it by the y coordinate(Call this Sum B). The last value in the row is a zero so you basically calculate 0×1 here. (Following matrix calculation rules). - Lastly add Sum A+Sum B to get the new x – coordinate, x'.

- Do the same with the last two rows, keeping in mind what it is you are actually doing.( How you actually are finding the new coordinates).

When you are finished you should be left with the new point (x',y') rotated 90 degrees counter-clockwise about the origin, like below.

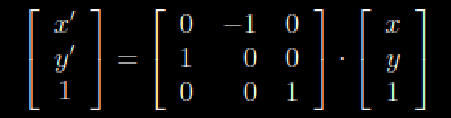
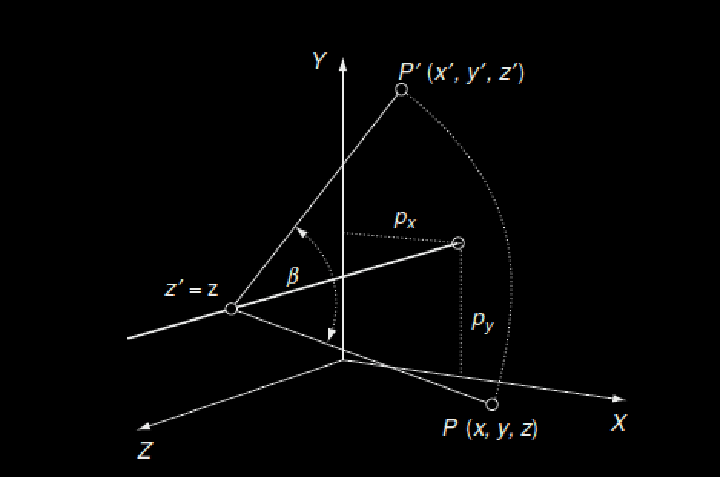
To rotate a point around another point , you could use the matrix beneath. What you are also seeing in the matrix beneath is the compensation that is made for the distance from the point of rotation to the point of origin in your coordinate system. Of course in 3D we rotate about an axis.

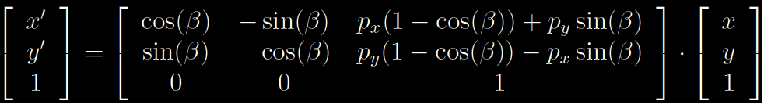
The rotation in itself is then extended to 3 dimensions by adding another row and another column, like you see here where the rotation is around the x- axis:

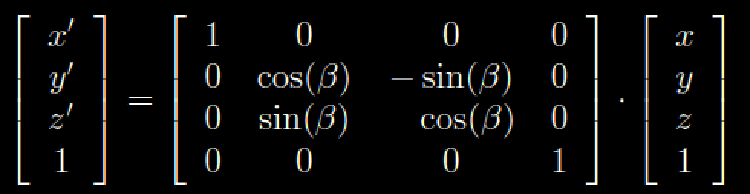
As for the 2D - action you can combine several translational matrices to calculate faster and more efficient. Going back to the top of the post, what you what you saw there were the matrices that calculate rotation for the three different axis x,y,z;

- Roll being the angle of rotation about the z -axis

- Pitch is the angle of rotation about the x -axis

- Yaw is the angle of rotation about the y-axis

All these can then be combined with a translate matrices(Move etc..) to make operations more effective. But first a note about axis terms. Remember that there will be difficulties if you mix right-handed and left-handed systems or which axis is up , when you program for a API. In Autodesk Maya, the default up – axis is 'y' and the coordinate system is right- handed by default.

So consider now translating and rotating a point into a new point:

...and an example of this in the diagram beneath, with the rotation and the hypothetical movement of the point from origin to (x'',y'',z'') new point.

Simplifying nature's occurrences is the way in which we manage to first grasp their complex processes. From attributing binary language value to 0's and 1's we carry this mentality over all the way to society's industrial production and technology. Architectural design is a field in which this is visually obvious. Simplifying to the degree of the straight euclidian angle is both a grossly errounous estimate but also a potential key to finding "simple" solutions to difficult questions. Nature does not produce 1 perfectly straight angle. Consider that fact for a minute.

I describe here one of several solutions to parsing a written language script into computer abstraction and further into Computer Graphics. This method has in it the flaws of gross over- simplification of natural processes, but that is not to say it is too simple. Instead it indeed opens other doors to artificial evolution that can not be acchieved in nature. I propose that we are inspired and guided by nature but we do not need to neccesarily reproduce it. The extensions and translations of the mathematical principles described earlier are parts of what make the foundation for Computer Graphics , and when on that subject the polygon is as good a place to start as any. Drawing a polygon (Here comes the process, from start to finish, through source code and everything) to act as the basis for a rewriting scheme, we can use lines or so- called edges.